行列の固有値を視覚イメージと行列式から素早く求める裏技【新発見】

大学数学の線形代数では「行列の固有値」を求める問題は必ず出てきます。正統派の解法は単純ですが、単に計算量が多くて時間が足りないという問題が発生します。そこで、その状況を改善するすごい裏技を紹介します。ただし、この方法は3,4次正方行列で有効なものです(2次は簡単、5次以降は正統派の方法でも解ける問題がほとんど)。

固有方程式は、行列Aに対して、$|\lambda E-A|=0$と表される方程式で、その解$\lambda$(複数)を行列Aの固有値と言います。

この記事では、3,4次正方行列の固有値(固有方程式)を楽に求める方法が分かります。答えを求めるのに使うのも、検算に使うのもどちらにも良いです！

※予備知識：行列式
※固有ベクトルの求め方、固有値自体の解説などは他サイトをご参照ください。需要があれば作成してみます。

3次正方行列の固有値を求める裏技
4次正方行列の固有値を求める裏技
n次正方行列での固有方程式で言えること
裏技を用いた計算
- 例：3次の場合
普通の計算の方が速い場合

3次正方行列の固有値を求める裏技

3次正方行列$A=\left(
\begin{array}{c}
a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}
\end{array}\right)$について考えます。

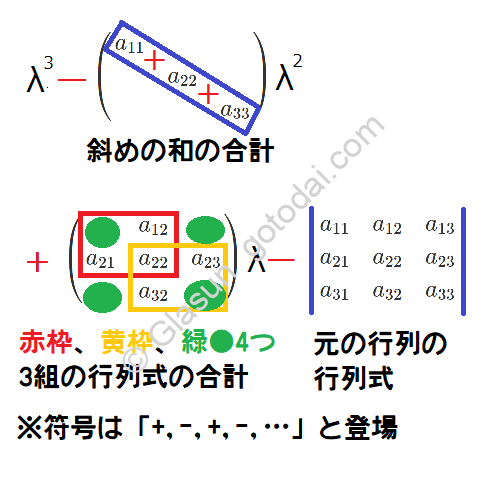
すべての固有値を解に持つ固有方程式を求めますが、通常の方法では非常に繁雑な計算になることもしばしばあります。しかし、固有方程式が楽に求まる方法があり、これさえ身に付ければ機械的に早く解くことができます！

最高次の一つ下の次数の係数で$tr(A)$が出てくることことや、定数項で$|A|$が出てくることは線形代数で検算法として紹介されるかもしれませんので、3次の場合では、符号が交互に変わることと1次の項の係数の特徴のみを抑えればよいわけです。

$\begin{equation} \begin{split} |\lambda E-A|&= \begin{vmatrix} \lambda-a_{11}&-a_{12}&-a_{13}\\ -a_{21}&\lambda-a_{22}&-a_{23}\\ -a_{31}&-a_{32}&\lambda-a_{33} \end{vmatrix} \\ &=\lambda ^3 -tr(A)\lambda ^2 +\left(\begin{vmatrix} a_{11}&a_{12}&\\ a_{21}&a_{22}&\\ && \end{vmatrix} +\begin{vmatrix} &&\\ &a_{22}&a_{23}\\ &a_{32}&a_{33} \end{vmatrix} +\begin{vmatrix} a_{11}&&a_{13}\\ &&\\ a_{31}&&a_{33} \end{vmatrix}\right)\lambda -|A| \end{split} \end{equation}$

固有値を求める問題では
①固有方程式を上の方法で求める。
②高次方程式を解く(組立除法)。
③すべての解が固有値となる。

証明

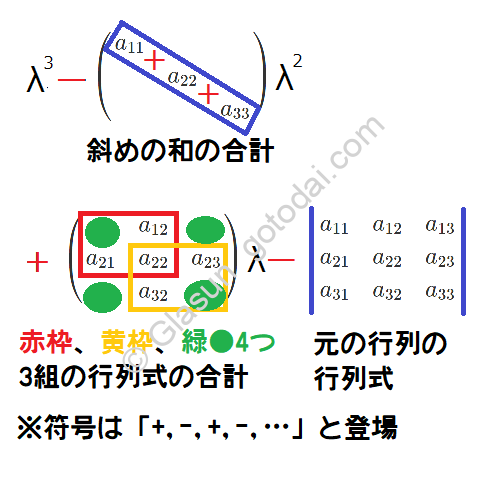
固有方程式の左辺の行列式$|\lambda E-A|$を展開して、$\lambda$の次数でまとめるしかありません。しかし、最高次の一つ下の次数の係数で$tr(A)$が出てくることや、定数項で$|A|$が出てくることを線形代数でなんとなく聞いたことがあれば、その項については答えの形が予測できると思います。

$\begin{equation} \begin{split} |\lambda E-A|&=\begin{vmatrix} \lambda-a_{11}&-a_{12}&-a_{13}\\ -a_{21}&\lambda-a_{22}&-a_{23}\\ -a_{31}&-a_{32}&\lambda-a_{33} \end{vmatrix}\\ &= \cdots \\ &=\lambda ^3 -\underbrace{(a_{11}+a_{22}+a_{33})}_{tr(A)}\lambda ^2 +\left\{(a_{11}a_{22}-a_{12}a_{21})+(a_{22}a_{33}-a_{23}a_{32})+(a_{11}a_{33}-a_{13}a_{31})\right\} \lambda -\underbrace{\left\{ a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{21}(a_{12}a_{33}-a_{13}a_{32})+a_{31}(a_{12}a_{23}-a_{13}a_{22})\right\}}_{|A|} \end{split} \end{equation}$

4次正方行列の固有値を求める裏技

精霊ソ・ノーダ

発展的な問題の答えが「(省略)」や「これは各自の課題としよう」という数学書でよくあるような流れはお話にならない。なので、ここではさらに難しい4次の場合も考えるとしよう。

4次正方行列$A=\left(
\begin{array}{c}
a_{11}&a_{12}&a_{13}&a_{14}\\
a_{21}&a_{22}&a_{23}&a_{24}\\
a_{31}&a_{32}&a_{33}&a_{34}\\
a_{41}&a_{42}&a_{43}&a_{44}
\end{array}\right)$について考えます。

$\begin{equation} \begin{split} |\lambda E-A|&= \begin{vmatrix} \lambda-a_{11}&-a_{12}&-a_{13}&-a_{14}\\ -a_{21}&\lambda-a_{22}&-a_{23}&-a_{24}\\ -a_{31}&-a_{32}&\lambda-a_{33}&-a_{34}\\ -a_{41}&-a_{42}&-a_{43}&\lambda-a_{44} \end{vmatrix} \\ &=\lambda ^4 -tr(A)\lambda ^3 +\left( \begin{vmatrix} a_{11}&a_{12}&&\\ a_{21}&a_{22}&&\\ &&&\\ &&& \end{vmatrix} +\begin{vmatrix} &&&\\ &a_{22}&a_{23}&\\ &a_{32}&a_{33}&\\ &&& \end{vmatrix} +\begin{vmatrix} &&&\\ &&&\\ &&a_{33}&a_{34}\\ &&a_{43}&a_{44} \end{vmatrix} +\begin{vmatrix} a_{11}&&a_{13}&\\ &&&\\ a_{31}&&a_{33}&\\ &&& \end{vmatrix} +\begin{vmatrix} &&&\\ &a_{22}&&a_{24}\\ &&&\\ &a_{42}&&a_{44} \end{vmatrix} +\begin{vmatrix} a_{11}&&&a_{14}\\ &&&\\ &&&\\ a_{41}&&&a_{44} \end{vmatrix} \right)\lambda ^2 -\left( \begin{vmatrix} a_{11}&a_{12}&a_{13}&\\ a_{21}&a_{22}&a_{23}&\\ a_{31}&a_{32}&a_{33}&\\ &&& \end{vmatrix} +\begin{vmatrix} a_{11}&a_{12}&&a_{14}\\ a_{21}&a_{22}&&a_{24}\\ &&&\\ a_{41}&a_{42}&&a_{44} \end{vmatrix} +\begin{vmatrix} a_{11}&&a_{13}&a_{14}\\ &&&\\ a_{31}&&a_{33}&a_{34}\\ a_{41}&&a_{43}&a_{44} \end{vmatrix} +\begin{vmatrix} &&&\\ &a_{22}&a_{23}&a_{24}\\ &a_{32}&a_{33}&a_{34}\\ &a_{42}&a_{43}&a_{44} \end{vmatrix} \right)\lambda +|A| \end{split} \end{equation}$

証明

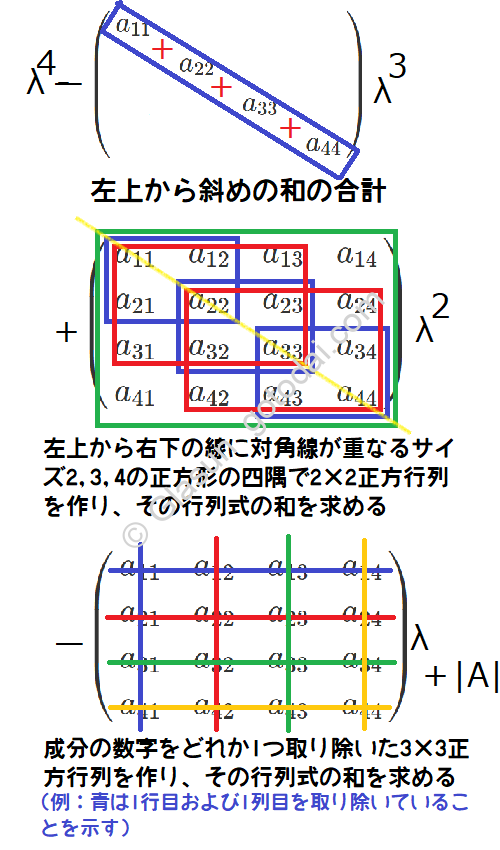
3次のときと同様にひたすら固有方程式を展開していきますが、定数項は$(-1)^n |A|$となることが決まっているので、$\lambda$が出てこない項は無視して次数別に並べていくことがコツです。

$\begin{equation} \begin{split} |\lambda E-A|&= \begin{vmatrix} \lambda-a_{11}&-a_{12}&-a_{13}&-a_{14}\\ -a_{21}&\lambda-a_{22}&-a_{23}&-a_{24}\\ -a_{31}&-a_{32}&\lambda-a_{33}&-a_{34}\\ -a_{41}&-a_{42}&-a_{43}&\lambda-a_{44} \end{vmatrix} \\ &= \cdots \\ &=\lambda ^4 -\underbrace{(a_{11}+a_{22}+a_{33}+a_{44})}_{tr(A)}\lambda ^3 +\left\{(a_{11}a_{22}-a_{12}a_{21})+(a_{22}a_{33}-a_{23}a_{32})+(a_{33}a_{44}-a_{34}a_{43})+(a_{11}a_{33}-a_{13}a_{31})+(a_{22}a_{44}-a_{24}a_{42})+(a_{11}a_{44}-a_{14}a_{41})\right\} \lambda ^2 -[\{ a_{11}(a_{22}a_{33}-a_{23}a_{32})-a_{21}(a_{12}a_{33}-a_{13}a_{32})+a_{31}(a_{12}a_{23}-a_{13}a_{22})\} +\{ a_{11}(a_{22}a_{44}-a_{24}a_{42})-a_{21}(a_{12}a_{44}-a_{14}a_{42})+a_{41}(a_{12}a_{24}-a_{14}a_{22})\} +\{ a_{11}(a_{33}a_{44}-a_{34}a_{43})-a_{31}(a_{13}a_{44}-a_{14}a_{43})+a_{41}(a_{13}a_{34}-a_{14}a_{33})\} +\{ a_{22}(a_{33}a_{44}-a_{34}a_{43})-a_{32}(a_{23}a_{44}-a_{24}a_{43})+a_{42}(a_{23}a_{34}-a_{24}a_{33})\}] \lambda +|A| \end{split} \end{equation}$

n次正方行列での固有方程式で言えること

4次のときの固有方程式をよく見てみると、各次数での係数についてあることに気が付きます。

各係数に付く符号は高い方($\lambda ^n$)から順に「+,-,+,-,…」
$\lambda ^k$の係数の構成要素は、1~nまでの数字からk個抜いた数字で作れる(n-k)次正方行列の行列式（ただし$\lambda ^n$の係数は1とする）
構成要素の個数は、k個の抜き方で$_n C_k$個

$tr(A)=|a_{11}|+|a_{22}|+\cdots$に注意しましょう(ここでは$|\cdots|$は絶対値の意味ではなく、1次正方行列の行列式と捉えてください)。

具体的に4次の場合で説明すると、
$(+)\lambda ^4 \cdots$1とする
$(-)\lambda ^3 \cdots$4つの数字から3つを抜いて作れる1次正方行列は、$_4 C_3 =4$通りできてそれら和となる
$(+)\lambda ^2 \cdots$4つの数字から2つを抜いて作れる2次正方行列は、$_4 C_2 =6$通りできてそれら和となる
$(-)\lambda ^1 \cdots$4つの数字から1つを抜いて作れる3次正方行列は、$_4 C_1 =4$通りできてそれら和となる
$(+)\lambda ^0 \cdots$4つの数字から0つを抜いて作れる4次正方行列は、$_4 C_0 =1$通りできてそれら和となる

(注)5次以上の代数方程式では解の公式が存在しないため、うまく数が選ばれていないと固有値が表せないことになります。

裏技を用いた計算

例：3次の場合

$A=\left(\begin{array}{c}
1&0&1\\
-1&2&1\\
1&-1&1\end{array}\right)$の固有値を求めよ。

固有方程式を作るところから始めます。各次数の係数を決めていきます。

$(+)\lambda ^3 \cdots$1
$(-)\lambda ^2 \cdots$左上から対角線上の数字を足していくと、1+2+1=4
$(+)\lambda ^1 \cdots$3通りの2次正方行列の行列式の和を考えて、
$\begin{vmatrix}1&0\\-1&2\end{vmatrix}+\begin{vmatrix}2&1\\-1&1\end{vmatrix}+\begin{vmatrix}1&1\\1&1\end{vmatrix}=2+3+0=5$
$(-)\lambda ^0 \cdots$$|A|$を求めて、2

よって、固有方程式は
$$\phi_{A}(\lambda)=\lambda ^3 -4\lambda ^2 +5\lambda -2=(\lambda -1)^2 (\lambda -2)=0$$
より、固有値は$\lambda=1(重解),2$

普通の計算の方が速い場合

典型的な例としては、$A=\left(\begin{array}{c} a_{11} & a_{12} & \dots & a_{1n} \\
& a_{22} & \dots & a_{2n} \\
& & \ddots & \vdots \\
& \Huge{0}& & a_{nn} \end{array}\right)$のような行列（三角行列）です。このとき
$|\lambda E-A|=(\lambda-a_{11})(\lambda-a_{22})\cdots(\lambda-a_{nn})$
より、$\lambda=a_{11},a_{22},\cdots,a_{nn}$となることは、正統派の方法で簡単に求まります。